For a while now I’ve been using my own C++ implementation of Knuth’s Dancing Links algorithm. The algorithm is quite fast for solving the 0-1 matrix exact cover problem. More importantly, a number of other combinatorial problems can be converted into an exact cover framework, such as finding latin square completions, enumerating latin bitrades, and computing the chromatic number and chromatic polynomial of graphs (those last two are from comments by Tom Boothby on the sage-devel mailing list).
The thread started by Tom inspired me to make my code public, license it with GPL, write a few doctests, and learn the necessary Cython to write a wrapper for my C++ code so that it would be usable from Sage. The code is available here, in particular dancing_links.sage (top level Sage wrapper), dancing_links.spyx (Cython code that calls my C++ code), and finally dancing_links.cpp (the actual solver).
Not surprisingly, the C++ version is a fair bit faster than the Python implementation adapted by Tom when used as a latin square solver for finding “greedy” critical sets:
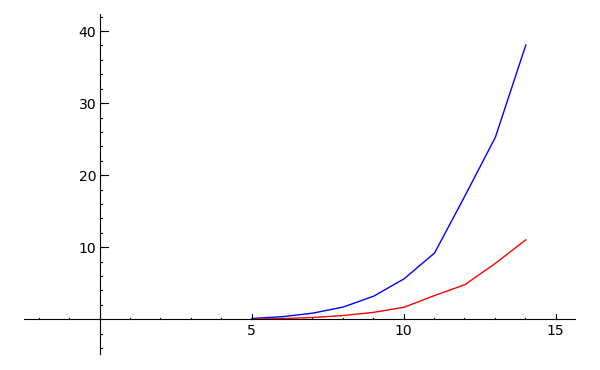
x-axis: \(n\), y-axis: number of seconds to compute the greedy critical set of \(B_n\) (addition table for \(Z_n\)), blue is Python, red is C++.