Some of my research is on dissections of triangles into equilateral triangles. Here’s an example:
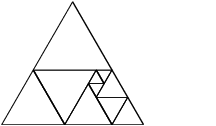
So the outer equilateral triangle is cut up into smaller equilateral triangles, and no triangles overlap except along a common edge or point.
One of the earliest references on triangle dissections is this paper: The Dissection of Equilateral Triangles into Equilateral Triangles, W.T.Tutte, Proceedings of the Cambridge Philosophical Society, Vol. 44, pages 464-82, 1948. There, Tutte showed a connection between equilateral triangle dissections and electrical networks. See also http://www.squaring.net/tri/twt.html and the paper The dissection of rectangles into squares – R. L. Brooks, C. A. B. Smith, A. H. Stone and W. T. Tutte; 312-340.
A perfect dissection has no two triangles of the same size in the same orientation (up or down). Tutte conjectured that the smallest perfect dissection has size 15, and some recent enumeration work shows this to be the case (a paper will come out soon with these results). Here are the two perfect dissections of size 15, and perfect dissections of size 16 and 17:
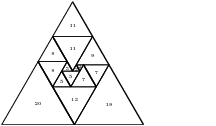
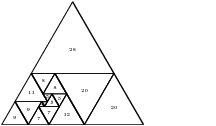
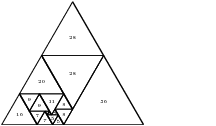
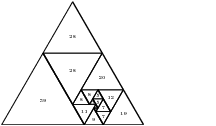
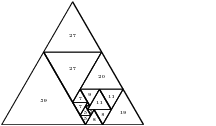
Those graphics are produced using PyX and Sage. Full PDFs are available here.