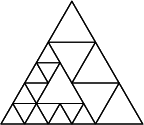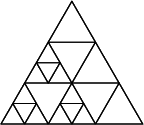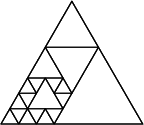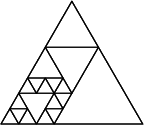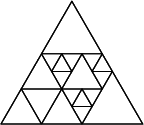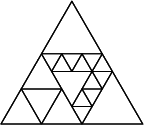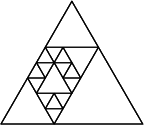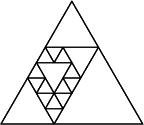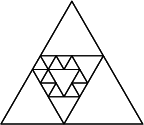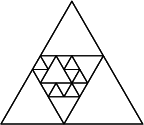A triangle dissection of an equilateral triangle is a way of dividing up a original triangle into smaller equilateral triangles, such that none of the smaller triangles overlap (for a few examples, scroll down in this post). Due to a known link between spherical latin bitrades and triangle dissections, we are able to enumerate triangle dissections exhaustively up to a certain size.
One way to calculate a canonical signature for each dissection is to take the list of triangles, the vertices of which live in \(\mathbb{Q}(\sqrt{3}) \times \mathbb{Q}(\sqrt{3})\), and take the sorted minimum sequence of sorted triples. We can write down a convenient representation (avoiding irrational numbers) by noting that elements of \(\mathbb{Q}(\sqrt{3})\) have the form \(a + b\sqrt{3}\) where \(a,b \in \mathbb{Q}\). For example, the first dissection shown below has the following signature:
0 0 0 0 1/1 2 0 0 1/12 1/6 0 0 0 1/12 0 0 1/12 1/6 0 0 0 1/4 0 0 1/12 1/12 0 0 1/12
1/6 0 0 1/6 1/4 0 0 1/12 1/6 0 0 0 1/4 0 0 1/12 1/3 0 0 0 1/6 0 0 1/6 1/4 0 0 1/12
1/3 0 0 1/6 1/6 0 0 1/6 1/4 0 0 1/4 1/3 0 0 1/6 1/4 0 0 1/12 1/3 0 0 0 5/12 0 0 1/12
1/4 0 0 1/12 5/12 0 0 1/4 7/12 0 0 1/12 1/4 0 0 1/4 1/3 0 0 1/6 5/12 0 0 1/4 1/4 0
0 1/4 1/3 0 0 1/3 5/12 0 0 1/4 1/3 0 0 0 5/12 0 0 1/12 1/2 0 0 0 1/3 0 0 1/3 1/2 0
0 1/6 2/3 0 0 1/3 1/3 0 0 1/3 1/2 0 0 1/2 2/3 0 0 1/3 5/12 0 0 1/12 1/2 0 0 0 7/12 0
0 1/12 1/2 0 0 0 7/12 0 0 1/12 2/3 0 0 0 1/2 0 0 1/6 2/3 0 0 0 5/6 0 0 1/6 1/2 0 0
1/6 2/3 0 0 1/3 5/6 0 0 1/6 2/3 0 0 0 5/6 0 0 1/6 1 0 0 0
(This signature can be converted to a PDF by echoing it as a single line to the Python script draw_dissection.py)
While double-checking my C++ implementation I found that my old Python code was finding 5 fewer dissections of order 18, when counting both separated and nonseparated dissections (separated dissections have interior vertices of degree 4, while nonseparated dissections have interior vertices of degree 4 or 6). It turned out to be the way that I was calculating a canonical signature. In the interest of saving space, my old Python code just stored a list of vertices, so naturally it lost information about whether a vertex was of degree 4 or 6. Surprisingly this caused no problems until order 18. The 5 pairs of vertex-equivalent dissections are shown below: