Knight on a chess board

Here is a well-known interview/code golf question: a knight is placed on a chess board. The knight chooses from its 8 possible moves uniformly at random. When it steps off the board it doesn’t move anymore. What is the probability that the knight is still on the board after $n$ steps?

We could calculate this directly but it’s more interesting to frame it as a Markov chain.

Calculation using the transition matrix Link to heading

Model the chess board as the tuples $\{ (r, c) \mid 0 \leq i, j \leq 7 \}$.

Here are the valid moves and a helper function to check if a move $(r,c) \rightarrow (u,v)$ is valid and if a cell is on the usual $8 \times 8$ chessboard:

moves = [(-2, 1), (-1, 2), (1, 2), (2, 1),
         (2,-1), (1,-2), (-1,-2), (-2,-1)]

def is_move(r, c, u, v):
    for m in moves:
        if (u, v) == (r + m[0], c + m[1]):
            return True
    return False

def on_board(x):
    return 0 <= x[0] < 8 and 0 <= x[1] < 8

The valid states are all the on-board positions plus the immediate off-board positions:

states = [(r, c) for r in range(-2, 8+2) for c in range(-2, 8+2)]

Now we can set up the transition matrix.

def make_matrix(states):
    """
    Create the transition matrix for a knight on a chess board
    with all moves chosen uniformly at random. When the knight
    moves off-board, no more moves are made.
    """

    # Handy mapping from (row, col) -> index into 'states'
    to_idx = dict([(s, i) for (i, s) in enumerate(states)])

    P = np.array([[0.0 for _ in range(len(states))] for _ in range(len(states))], dtype='float64')
    assert P.shape == (len(states), len(states))

    for (i, (r, c)) in enumerate(states):
        for (j, (u, v)) in enumerate(states):
            # On board, equal probability to each destination, even if goes off board.
            if on_board((r, c)):
                if is_move(r, c, u, v):
                    P[i][j] = 1.0/len(moves)

            # Off board, no more moves.
            else:
                if (r, c) == (u, v): # terminal state
                    P[i][j] = 1.0
                else:
                    P[i][j] = 0.0

    return to_idx, P

We can visualise the transition graph using graphviz (full code here):

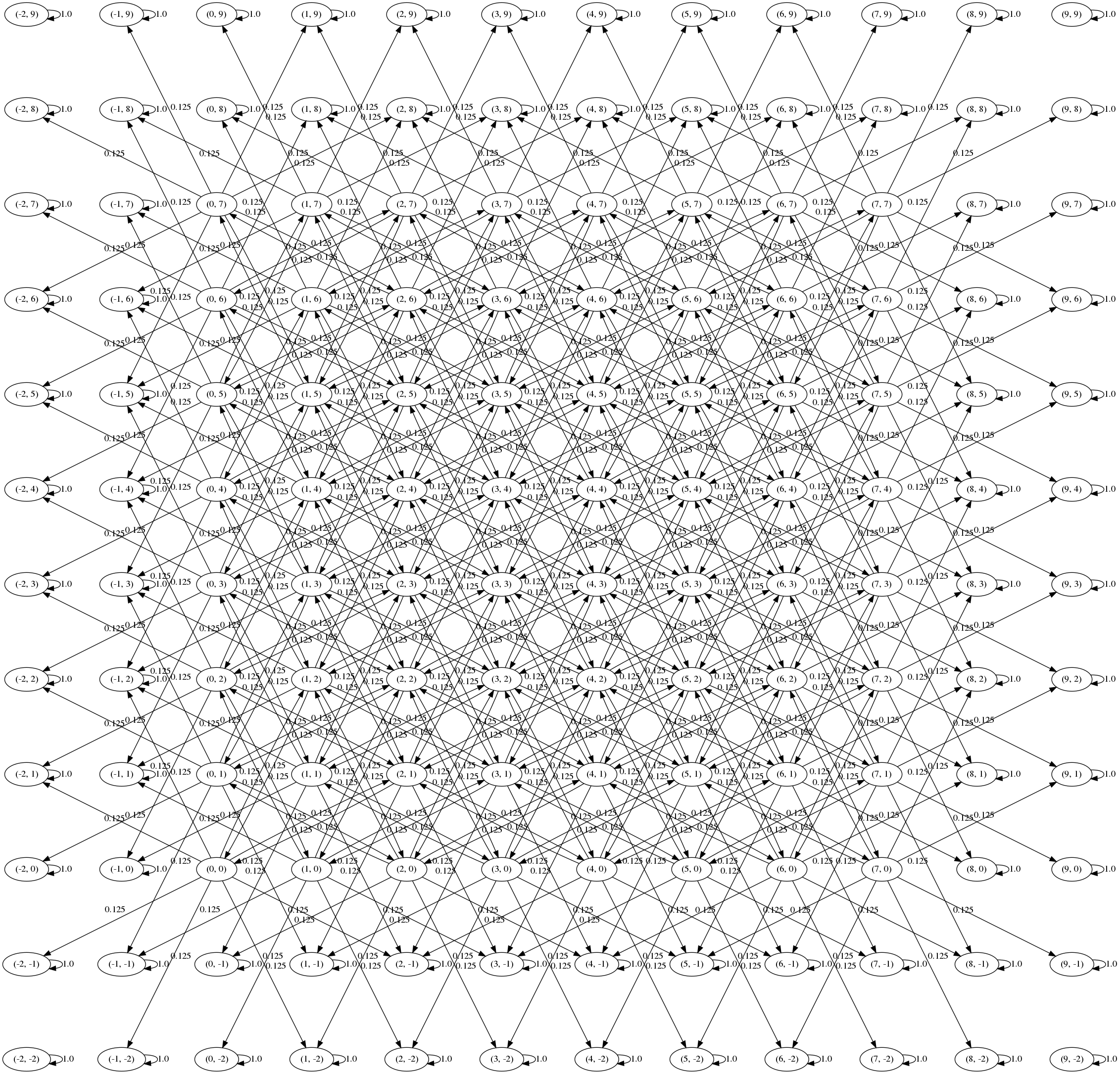
Oops! The corners aren’t connected to anything so we have 5 communicating classes (the 4 corners plus the rest). We never reach these nodes from any of the starting positions so we can get rid of them:

corners = [(-2,9), (9,9), (-2,-2), (9,-2)]
states = [(r, c) for r in range(-2, 8+2) for c in range(-2, 8+2) if (r,c) not in corners]

Here’s the new transition graph:

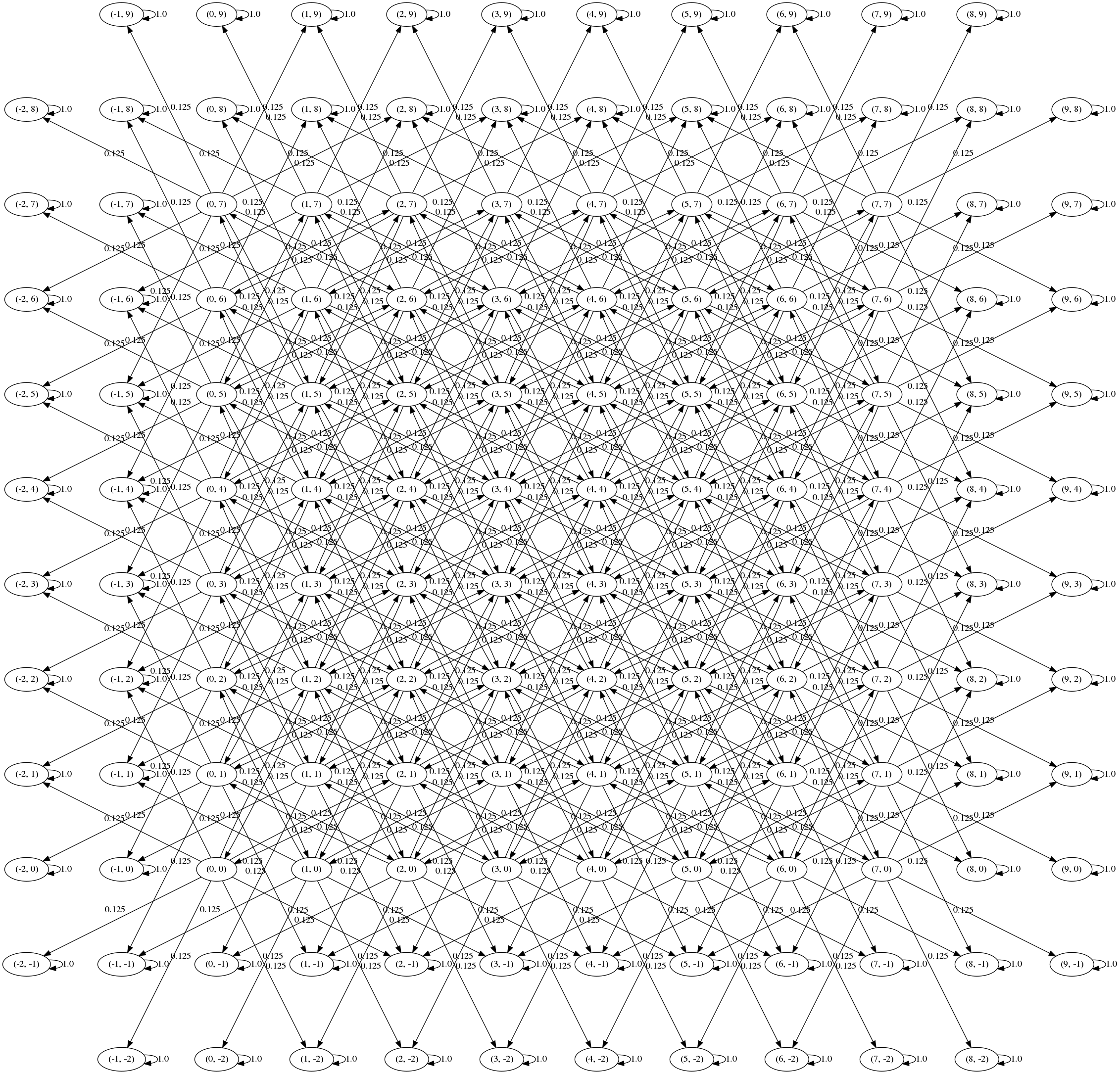
Intuitively, the knights problem is symmetric, and this graph is symmetric, so it’s likely that we’ve set things up correctly.

Let $X_0$, $X_1$, $\ldots$, $X_n$ be the positions of the knight. Then then probability of the knight moving from state $i$ to $j$ in $n$ steps is

So the probability of being on the board after $n$ steps, starting from $i$, will be

where $\mathcal{B}$ is the set of on-board states. This is easy to calculate using Numpy:

start = (3, 3)
n     = 5

idx = to_idx[start]
Pn = matrix_power(P, n)
pr = sum([Pn[idx][r] for (r, s) in enumerate(states) if on_board(s)])

For this case we get probability $0.35565185546875$.

Here are a few more calculations:

start: (0, 0)	n: 0	Pr(on board): 1.0
start: (3, 3)	n: 1	Pr(on board): 1.0
start: (0, 0)	n: 1	Pr(on board): 0.25
start: (3, 3)	n: 4	Pr(on board): 0.48291015625
start: (3, 3)	n: 5	Pr(on board): 0.35565185546875
start: (3, 3)	n: 100	Pr(on board): 5.730392258771815e-13

It’s always good to do a quick Monte Carlo simulation to sanity check our results:

def do_n_steps(start, n):
    current = start

    for _ in range(n):
        move = random.choice(moves)
        new = (current[0] + move[0], current[1] + move[1])
        if not on_board(new): break
        current = new

    return on_board(new)

N_sims = 10000000
n = 5

nr_on_board = 0

for _ in range(N_sims):
    if do_n_steps((3,3), n): nr_on_board += 1

print('pr on board from (3,3) after 5 steps:', nr_on_board/N_sims)

The estimate is fairly close to the value we got from taking power of the transition matrix:

pr on board from (3,3) after 5 steps: 0.3554605

Absorbing states Link to heading

An absorbing state of a Markov chain is a state that, once entered, cannot be left. In our problem the absorbing states are precisely the off-board states.

A natural question is: given a starting location, how many steps (on average) will it take the knight to step off the board?

With a bit of matrix algebra we can get this from the transition matrix $(\boldsymbol{P}$. Partition $\boldsymbol{P}$ by the state type: let $\boldsymbol{Q}$ be the transitions of transient states (here, these are the on-board states to other on-board states); let $\boldsymbol{R}$ be transitions from transient states to absorbing states (on-board to off-board); and let $\boldsymbol{I}$ be the identity matrix (transitions of the absorbing states). Then $\boldsymbol{P}$ can be written in block-matrix form:

We can calculate powers of $\boldsymbol{P}$:

In general:

We want to calculate \( \lim_{n \rightarrow \infty} \boldsymbol{P}^n \) since this will tell us the long-term probability of moving from one state to another. In particular, the top-right block will tell us the long-term probability of moving from a transient state to an absorbing state.

Here is a handy result from matrix algebra:

Lemma. Let \( \boldsymbol{A} \) be a square matrix with the property that \( \boldsymbol{A}^n \rightarrow \mathbf{0} \) as \( n \rightarrow \infty \). Then \( \sum_{n=0}^\infty = (\boldsymbol{I} - \boldsymbol{A})^{-1}. \)

Applying this to the block form gives:

where \( \lim_{n \rightarrow \infty} \boldsymbol{Q}^n = 0 \) since all of the entries in \( \boldsymbol{Q} \) are transient.

The top-right corner also contains the fundamental matrix as defined in the following theorem:

Theorem Consider an absorbing Markov chain with \( t \) transient states. Let \( \boldsymbol{F} \) be a \( t \times t \) matrix indexed by the transient states, where \( \boldsymbol{F}_{i,j} \) is the expected number of visits to \( j \) given that the chain starts in \( i \). Then \( \boldsymbol{F} = (\boldsymbol{I} - \boldsymbol{Q})^{-1}. \)

Taking the row sums of \( \boldsymbol{F} \) gives the expected number of steps \( a_i \) starting from state \( i \) until absorption (i.e. we count the number of visits to each transient state before eventual absorption):

Back in our Python code, we can rearrange the states vector so that the transition matrix is appropriately partitioned. Taking the \( \boldsymbol{Q} \) matrix is very quick using Numpy’s slicing notation:

states = [s for s in states if on_board(s)]
       + [s for s in states if not on_board(s)]
(to_idx, P) = make_matrix(states)

# k states
k = len(states)

# t transient states
t = len([s for s in states if on_board(s)])

Q = P[:t, :t]
assert Q.shape == (t, t)
assert Q.shape == (64, 64)

F = linalg.inv(np.eye(*Q.shape) - Q)

# example calculation for a_(3,3):

state = (3, 3)
print(F[to_idx[state], :].sum())

Again, compare to a Monte Carlo simulation to verify that the numbers are correct:

start: (0, 0)	Avg nr steps to absorb (MC): 1.9527606
start: (0, 0)	Avg nr steps (F matrix):     1.9525249995183136

start: (3, 3)	Avg nr steps to absorb (MC): 5.4187947
start: (3, 3)	Avg nr steps (F matrix):     5.417750460813215

So, on average, if we start in the corner \( (0,0) \) we will step off the board after \( 1.95 \) steps; if we start in the centre at \( (3,3) \) we will step off the board after \( 5.41 \) steps.

Further reading Link to heading

The theoretical parts of this blog post follow the presentation in chapter 3 of Introduction to Stochastic Processes with R (Dobrow).

Source code: github.com/carlohamalainen/playground/tree/master/python/knight-random-walk.